안녕하세요. J4J입니다.
이번 포스팅은 정렬 알고리즘 중 선택 정렬에 대해 적어보는 시간을 가져보려고 합니다.
선택 정렬이란?
선택 정렬은 매 회전마다 인덱스를 탐색하여 최솟값을 처음부터 순서대로 집어넣는 정렬 방식입니다.
예를 들어 길이가 5인 배열이 있다고 가정하면 정렬되는 순서는 다음과 같습니다.
1-1. 0번 인덱스를 임시 최솟값으로 지정합니다.
1-2. 1~4번 인덱스를 탐색하여 임시 최솟값보다 작은 게 존재할 시 0번 인덱스와 위치를 변경합니다.
2-1. 1번 인덱스를 임시 최솟값으로 지정합니다.
2-2. 2~4번 인덱스를 탐색하여 임시 최솟값보다 작은 게 존재할 시 1번 인덱스와 위치를 변경합니다.
.
.
.
4-1. 3번 인덱스를 임시 최솟값으로 지정합니다.
4-2. 4번 인덱스를 탐색하여 임시 최솟값보다 작은 게 존재할 시 3번 인덱스와 위치를 변경합니다.
구현 코드 (Java)
package sorting;
import java.util.Arrays;
public class SelectionSort {
public static void main(String[] args) {
int intArray[] = new int[]{7, 3, 15, 11, 1};
for(int i=0; i<intArray.length-1; i++) {
int minIndex = i; // 시작 값을 임시 최솟값으로 지정
for(int j=i+1; j<intArray.length; j++) {
if(intArray[minIndex] > intArray[j]) { // j번째 값이 임시 최솟값보다 작다면
minIndex = j; // 임시 최솟값 인덱스 변경
}
}
// 시작 값과 최솟값 위치 변경
int temp = intArray[i];
intArray[i] = intArray[minIndex];
intArray[minIndex] = temp;
}
System.out.println(Arrays.toString(intArray)); // [1, 3, 7, 11, 15]
}
}

특징
- 구현이 쉽습니다.
- 불안정 정렬(unstable sort)입니다. (정렬 전과 후를 비교했을 때 동일 값들끼리 순서가 변경될 수 있습니다.)
- 제자리 정렬(in-place sort)입니다. (값이 담겨있는 것을 제외하고는 추가적인 공간을 사용하지 않습니다.)
- 시간 복잡도가 O(N^2)입니다
시간 복잡도가 O(N^2)인 이유는 구현할 때 첫 번째 for문이 n-1번만큼 순회하며 두 번째 for문을 n-1번, n-2번, ... , 2번, 1번만큼 순회하고 계산하면 (n-1) + (n-2) + ... + (2) + (1) = n(n-1)/2입니다. (결과값에 대해 이해가 안 되시면 구글에 "시그마 k" 검색)
결과값의 최고차항이 n^2이기 때문에 시간 복잡도가 O(N^2)입니다. (단순히 n만큼 순회하는 for문이 2개여서 O(N^2)이다 생각하셔도 됩니다.)
번외
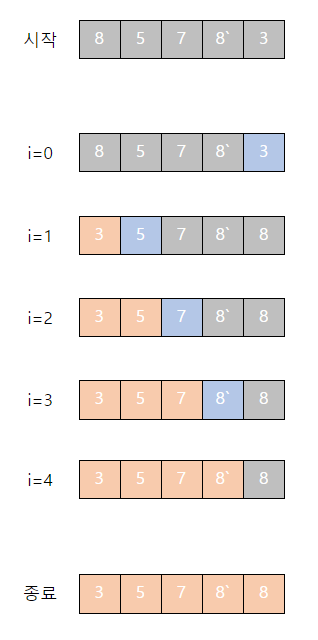
해당 포스팅을 적으면서 항상 안정 정렬처럼 정렬이 되는 것 같은데 어떻게 불안정 정렬일까에 대해 고민을 했는데 다음과 같은 케이스 때문에 불안정 정렬에 속합니다.
동일 값은 8이며 8과 8`로 서로를 구분하겠습니다.
정렬 전에는 8이 8`보다 앞에 있지만 정렬 후에는 8이 8`보다 뒤에 있는 것을 확인할 수 있습니다.
정리
이상으로 선택 정렬에 대해 간단하게 알아보는 시간이었습니다.
읽어주셔서 감사합니다.
'Algorithm > Algorithm' 카테고리의 다른 글
| [Algorithm] 순열(Permutation) (0) | 2021.01.11 |
|---|---|
| [Algorithm] 정렬 - 퀵 정렬(Quick Sort) (0) | 2021.01.10 |
| [Algorithm] 정렬 - 합병 정렬(Merge sort) (0) | 2021.01.09 |
| [Algorithm] 정렬 - 삽입 정렬(Insertion Sort) (0) | 2021.01.09 |
| [Algorithm] 정렬(Sorting) (0) | 2021.01.03 |



댓글