개요
안녕하세요. J4J입니다.
이번 포스팅은 너비 우선 탐색(BFS)에 대해 적어보는 시간을 가져보려고 합니다.
너비 우선 탐색이란?
너비 우선 탐색이란 그래프 탐색 기법 중 하나로 한 번 탐색을 시작한 정점에 연결된 모든 정점을(깊이가 같은 정점) 탐색한 뒤 다른 깊이에 있는 정점을 탐색하는 기법입니다.
추가적으로 그래프 탐색에 대해서도 설명드리면 한 정점을 시작으로 다른 존재하는 모든 정점을 한 번씩 방문하는 탐색을 그래프 탐색이라고 합니다.
사용 목적
너비 우선 탐색의 사용 목적은 시작 정점부터 다른 정점까지의 최단 거리를 구하기 위해 사용됩니다.
너비 우선 탐색과 많이 비교되는 깊이 우선 탐색은 최대한 깊게 가는 것을 목적으로 구현되기 때문에 값이 존재하는지 확인하기 위해 사용되지만 너비 우선 탐색은 시작 정점을 기준으로 원(?)처럼 퍼져나가기 때문에 목표 지점을 처음 방문하게 되면 가장 짧게 방문하는 케이스가 됩니다.
이런 이유로 최단 거리를 구할 때 보통 깊이 우선 탐색보다는 너비 우선 탐색을 많이 사용합니다.
그림 예시

너비 우선 탐색은 구현할 때 현재 정점의 인접한 정점들을 queue에 담아두는 특성이 있습니다.
위와 같은 그래프가 존재할 때 queue에 담아두는 것을 생각하며 0번 정점부터 너비 우선 탐색을 할 경우 다음과 같은 결과가 나옵니다.
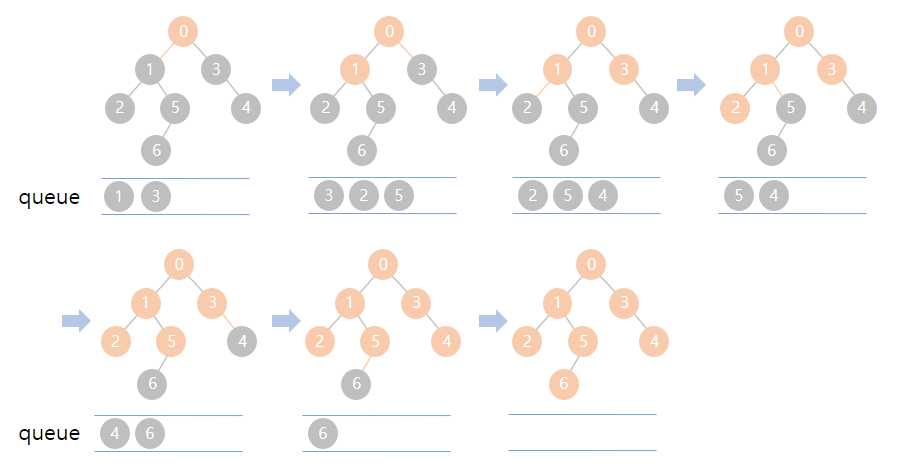
간단히 설명을 하면 다음과 같습니다.
1-1. 0번 정점에서 갈 수 있는 정점은 1번, 3번이 있습니다.
1-2. 1번, 3번은 둘 다 방문한 적이 없기 때문에 queue에 담아둡니다.
2-1. queue의 front를 꺼내면 1이 나옵니다.
2-2. 1번 정점에서 갈 수 있는 정점은 0번, 2번, 5번이 있습니다.
2-3. 0번은 이미 방문했고 2번, 5번은 방문한 적이 없기 때문에 queue에 담아둡니다.
3-1. queue의 front를 꺼내면 3이 나옵니다.
3-2. 3번 정점에서 갈 수 있는 정점은 0번, 4번이 있습니다.
3-3. 0번은 이미 방문했고 4번은 방문한 적이 없기 때문에 queue에 담아둡니다.
.
.
.
6-1. queue의 front를 꺼내면 4가 나옵니다.
6-2. 4번 정점에서 갈 수 있는 정점은 3번이 있습니다.
6-3. 3번은 이미 방문했기 때문에 더 이상 아무 동작도 하지 않습니다.
7-1. queue의 front를 꺼내면 6이 나옵니다.
7-2. 6번 정점에서 갈 수 있는 정점은 5번이 있습니다.
7-3. 5번은 이미 방문했기 때문에 더 이상 아무 동작도 하지 않습니다.
8-1. queue에 값이 존재하지 않기 때문에 실행을 종료합니다.
이와 같은 결과가 나오도록 코드를 구현하면 다음과 같습니다.
구현 코드 - 인접 행렬 (Java)
package graph;
import java.util.LinkedList;
import java.util.Queue;
public class BreadthFirstSearchArray {
public static void main(String[] args) {
int N = 7; // 정점의 갯수
boolean[][] graph = new boolean[N][N]; // true면 길(간선)이 존재, false면 길(간선)이 없음
addEdge(graph, 0, 1);
addEdge(graph, 0, 3);
addEdge(graph, 1, 2);
addEdge(graph, 1, 5);
addEdge(graph, 5, 6);
addEdge(graph, 3, 4);
boolean visited[] = new boolean[N]; // 정점의 방문 여부 / true면 방문, false면 미 방문
Queue<Integer> queue = new LinkedList<Integer>();
queue.add(0);
System.out.print("방문 순서: ");
while(!queue.isEmpty()) {
int index = queue.poll(); // 큐의 front에 있는 값 가져오기
if(visited[index]) { // 이미 방문한 index라면 되돌아가기
continue;
}
System.out.print(index + " "); // 방문 순서: 0 1 3 2 5 4 6
visited[index] = true; // 방문 체크
for(int i=0; i<N; i++) {
if(!visited[i] && graph[index][i]) { // 아직 방문하지 않고 길(간선)이 존재할 경우
queue.add(i);
}
}
}
}
public static void addEdge(boolean[][] graph, int u, int v) { // 길(간선) 추가
graph[u][v] = graph[v][u] = true;
}
}
구현 코드 - 인접 리스트 (Java)
package graph;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
public class BreadthFirstSearchList {
public static void main(String[] args) {
int N = 7; // 정점의 갯수
List<Integer> graph[] = new List[N];
for(int i=0; i<graph.length; i++) { // 초기화
graph[i] = new ArrayList<Integer>();
}
addEdge(graph, 0, 1);
addEdge(graph, 0, 3);
addEdge(graph, 1, 2);
addEdge(graph, 1, 5);
addEdge(graph, 5, 6);
addEdge(graph, 3, 4);
boolean visited[] = new boolean[N]; // 정점의 방문 여부 / true면 방문, false면 미 방문
Queue<Integer> queue = new LinkedList<Integer>();
queue.add(0);
System.out.print("방문 순서: ");
while(!queue.isEmpty()) {
int index = queue.poll(); // 큐의 front에 있는 값 가져오기
if(visited[index]) { // 이미 방문한 index라면 되돌아가기
continue;
}
System.out.print(index + " "); // 방문 순서: 0 1 3 2 5 4 6
visited[index] = true; // 방문 체크
for(int i=0; i<graph[index].size(); i++) {
int nextIndex = graph[index].get(i);
if(!visited[nextIndex]) { // 아직 방문하지 않을 경우
queue.add(nextIndex);
}
}
}
}
public static void addEdge(List<Integer> graph[], int u, int v) { // 길(간선) 추가
graph[u].add(v);
graph[v].add(u);
}
}
시간 복잡도
인접 행렬의 시간 복잡도는 O(N^2)입니다.
코드를 보시면 while문에서 아직 방문하지 않은 정점일 경우 for문을 이용하여 N번만큼 탐색을 합니다.
그리고 아직 방문하지 않은 정점일 경우만 while문 안의 for문이 실행되기 때문에 for문이 실행되는 경우는 정점의 총 개수인 N번입니다.
결과적으로 N번만큼 실행되는 for문을 N번 방문하기 때문에 N x N = N^2이라는 값이 나옵니다.
인접 리스트의 시간 복잡도는 O(E)입니다.
여기서 E는 길(간선)의 개수를 의미합니다.
코드를 보시면 인접 행렬과 동일하게 while문에서 아직 방문하지 않은 정점일 경우 for문을 이용하여 해당 정점에 연결된 길(간선)만큼 탐색을 합니다.
또한 방문하지 않은 정점일 경우만 for문이 실행되기 때문에 for문이 실행되는 경우는 정점의 총 개수인 N번입니다.
결과적으로 정점에 연결된 길(간선)만큼 탐색을 하는 for문을 N번 방문하는 것은 모든 정점의 개수를 의미하기 때문에 O(E)라는 시간이 걸립니다.
참고적으로 위의 코드에서 E값은 12입니다.
왜냐하면 간선의 개수는 6이지만 양방향으로 되어있기 때문에 2번씩 접근되어 6 x 2 = 12라는 값이 나옵니다.
또한 모든 정점에 모든 간선이 존재한다면 개수는 총 N^2 - N입니다. (자기 자신에게 가는 경우 제외)
그리고 이 값은 E와 동일하기 때문에 N^2 - N ≥ E라는 값이 나오고 O(N^2) ≥ O(N+E)라는 식이 성립됩니다.
정리
이상으로 너비 우선 탐색(BFS)에 대해 간단하게 알아보는 시간이었습니다.
읽어주셔서 감사합니다.
'Algorithm > Algorithm' 카테고리의 다른 글
| [Algorithm] MST - 프림 알고리즘(Prim Algorithm) (0) | 2021.01.27 |
|---|---|
| [Algorithm] 최소 신장 트리(MST, Minimum Spanning Tree) (0) | 2021.01.24 |
| [Algorithm] 깊이 우선 탐색(DFS, Depth First Search) (0) | 2021.01.18 |
| [Algorithm] 이분탐색(Binary Search) (0) | 2021.01.17 |
| [Algorithm] 부분집합(Subset) (0) | 2021.01.14 |




댓글