개요
안녕하세요. J4J입니다.
이번 포스팅은 크루스칼 알고리즘에 대해 적어보는 시간을 가져보려고 합니다.
크루스칼 알고리즘이란?
크루스칼 알고리즘은 대표적인 MST 구현 알고리즘 중 하나로 정점들 간의 연결된 길(간선)의 가중치를 작은 순서대로 선택하며 MST를 만드는 기법입니다.
예를 들어 A, B, C, D, E 정점이 있다고 가정해보겠습니다.
A ↔ C 가중치: 3
A ↔ D 가중치: 5
B ↔ C 가중치: 4
B ↔ D 가중치: 4
C ↔ E 가중치: 2
D ↔ E 가중치: 1
일때 다음과 같은 순서로 가중치를 선택합니다.
1-1. 가중치가 1로 가장 작은 D ↔ E 간선을 임의로 선택합니다.
1-2. 선택된 임의의 간선으로 MST를 유지하기 때문에 최종적으로 선택합니다.
2-1. 가중치가 2로 그 다음 가장 작은 C ↔ E 간선을 임의로 선택합니다.
2-2. 선택된 임의의 간선으로 MST를 유지하기 때문에 최종적으로 선택합니다.
3-1. 가중치가 3로 그 다음 가장 작은 A ↔ C 간선을 임의로 선택합니다.
3-2. 선택된 임의의 간선으로 MST를 유지하기 때문에 최종적으로 선택합니다.
4-1. 가중치가 4로 그 다음 가장 작은 B ↔ C 간선을 임의로 선택합니다.
4-2. 선택된 임의의 간선으로 MST를 유지하기 때문에 최종적으로 선택합니다.
5-1. 선택된 가중치가 (총 노드의 개수 - 1)이기 때문에 실행을 종료합니다.
그림 예시
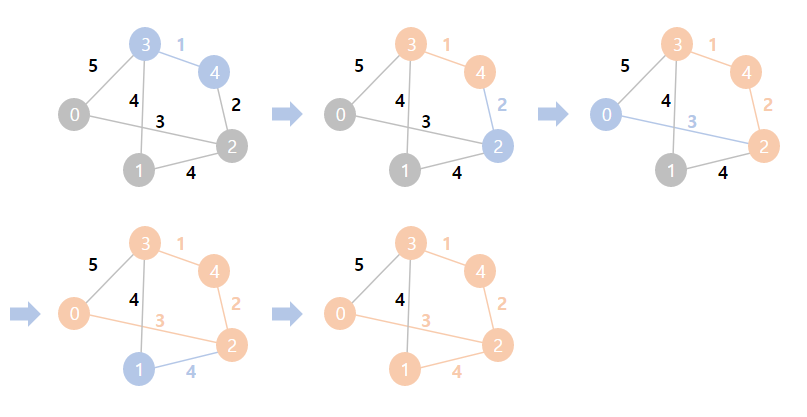
위의 순서와 동일한 상황을 그림으로 표현하면 다음과 같습니다. (A: 0, B: 1, C: 2, D: 3, E: 4)

구현 코드 (Java)
크루스칼 알고리즘의 구현은 서로소 집합(Disjoint Set) 자료구조를 표현하기 위해 사용되는 Union-Find 알고리즘을 사용하여 구현합니다.
package mst;
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;
public class Kruskal {
public static void main(String[] args) {
int N = 5; // 정점의 갯수
List<Node> graph = new ArrayList<Node>(); // 정점 간 가중치 저장
int parent[] = new int[N]; // 상위 정점 저장
int rank[] = new int[N]; // 정점 높이 저장
int sumWeight = 0; // 가중치의 합
int weightCount = 0; // 선택된 가중치 개수
// 가중치 추가
add(0, 2, 3, graph);
add(0, 3, 5, graph);
add(1, 2, 4, graph);
add(1, 3, 4, graph);
add(2, 4, 2, graph);
add(3, 4, 1, graph);
for(int i=0; i<N; i++) { // parent를 자기자신으로 초기화
parent[i] = i;
}
Collections.sort(graph, new Comparator<Node>() { // 가중치 오름차순으로 정렬
@Override
public int compare(Node o1, Node o2) {
return o1.weight - o2.weight;
}
});
for(int i=0; i<graph.size(); i++) {
if(weightCount >= N-1) { // 선택된 가중치의 개수가 N-1개가 되면 종료
break;
}
Node node = graph.get(i);
int u = node.u;
int v = node.v;
while(parent[u] != u) { // u정점의 최상위 부모 정점 구하기
u = parent[u];
}
while(parent[v] != v) { // v정점의 최상위 부모 정점 구하기
v = parent[v];
}
if(u != v) { // 가장 높은 부모 정점이 같지 않을 경우
if(rank[u] > rank[v]) { // u정점이 v정점보다 최상위 부모 높이가 클 경우
parent[v] = u;
} else if(rank[v] > rank[u]) { // v정점이 u정점보다 최상위 부모 높이가 클 경우
parent[u] = v;
} else { // 최상위 부모 높이가 서로 같을 경우 임의로 하나 높이기
rank[u]++;
parent[v] = u;
}
sumWeight = sumWeight + node.weight; // 가중치 더하기
weightCount++; // 가중치 선택 개수 증가
}
}
System.out.println("가중치의 합: " + sumWeight); // 가중치의 합: 10
}
public static void add(int u, int v, int weight, List<Node> graph) {
graph.add(new Node(u, v, weight));
}
private static class Node {
int v, u; // 두 정점
int weight; // 가중치
public Node(int v, int u, int weight) {
this.v = v;
this.u = u;
this.weight = weight;
}
}
}
시간 복잡도
Union-Find를 이용하여 크루스칼 알고리즘의 시간 복잡도는 퀵 정렬, 합병 정렬과 같은 효율적인 정렬방법을 사용하면 O(ElogE)입니다.
여기서 E는 길(간선)의 총 개수를 의미합니다.
위의 코드를 보면 graph에 간선의 총 개수만큼 저장됩니다.
그리고 자바에서 제공해주는 Sort메서드를 이용하기 때문에 정렬과정에서 ElogE만큼의 시간이 소요됩니다.
for문은 총 E만큼 순회가 되고 for문 내부에 있는 while문은 logN만큼 시간이 소요됩니다.
여기서 알고 가셔야 될 점은 Union-Find가 진행되며 트리가 구성될 때 한 쪽에 쏠림 현상이 발생될 경우 N만큼의 시간이 소요되기 때문에 결과적으로 while문 내부는 EN만큼의 시간이 소요됩니다.
하지만 위의 코드는 한쪽 쏠림 현상이 발생되지 않고 rank에 따라 최적화가 되기 때문에 logN만큼의 시간이 소요됩니다.

결과적으로 정렬할 때 ElogE, while문에서는 ElogN의 시간이 필요하고 E는 보통 N보다 크기 때문에 O(ElogE)라는 시간 복잡도가 나오게 됩니다.
특징
1. 크루스칼 알고리즘은 길(간선)을 순회하는 기법을 사용하기 때문에 정점과 상관없이 길(간선)의 개수가 적은 편일 때 주로 사용합니다.
2. 그리디(Greedy) 알고리즘 기법입니다. (각 상황별 가장 좋아보이는 선택지를 고릅니다.)
3. Union-Find를 이용하여 구현됩니다.
정리
이상으로 크루스칼 알고리즘에 대해 간단하게 알아보는 시간이었습니다.
읽어주셔서 감사합니다.
'Algorithm > Algorithm' 카테고리의 다른 글
| [Algorithm] 최단 경로 탐색(Shortest Path) - 플로이드 워셜 알고리즘(Floyd-Warshall Algorithm) (0) | 2021.02.01 |
|---|---|
| [Algorithm] 최단 경로 탐색(Shortest Path) - 다익스트라 알고리즘(Dijkstra Algorithm) (0) | 2021.01.31 |
| [Algorithm] MST - 프림 알고리즘(Prim Algorithm) (0) | 2021.01.27 |
| [Algorithm] 최소 신장 트리(MST, Minimum Spanning Tree) (0) | 2021.01.24 |
| [Algorithm] 너비 우선 탐색(BFS, Breadth First Search) (0) | 2021.01.21 |




댓글